How to Write a JWST Proposal for Transiting Exoplanet Science
- 1 Initial Setup
- 2 What accuracy in planet properties do I need?
- 3 What tools do I need? How do I use them?
- 4 How can I "prove" observability?
- 4.1 Can an atmosphere be detected: Addressing cloud concerns and quantifying statistical significance in transmission
- 4.2 Can an atmosphere be detected: Addressing unknown climate and quantifying statistical significance in emission
- 4.3 Can a specific molecule be detected?
- 4.4 Can any physical parameters be constrained? Information content theory for initial constraint estimates
Initial Setup¶
If you are reading this chances are you've done these, but you can never be too sure.
git clone https://github.com/natashabatalha/propexo.git
cd propexo
conda env create -f propexo.yml
conda activate propexo
jupyter notebook
This tutorial has three big package dependencies: 1) PandExo, 2) PICASO, 3)CHIMERA
Each of these depend on pretty hefty reference data packages that include things such as opacities, chemistry, JWST reference data.
Download Files and Fill in the Blank Below (Requires ~12 Gb)¶
This is a lot of data so I recommend downloading it early, and ensuring you have enough storage space.
- PandExo Reference Data - 2.2 Gb: will need to unzip
- Stellar Data Used in PandExo, PICASO, and CHIMERA - 877 Mb: will need to unzip
- Cross sections and chemistry for CHIMERA - 4 Gb: will need to unzip
- Cross sections for PICASO - 6 Gb
import os
# STEP 1: PandExo Reference Data
# SET YOUR OWN PATH to "/pandeia_data-1.5.1"
# e.g. mine is "/Users/meialua/Documents/data/pandeia_data-1.5.1"
os.environ['pandeia_refdata'] =
# STEP 2
#SET YOUR OWN PATH to stellar data "/grp/hst/cdbs"
#e.g. mine is "/Users/nbatalh1/Documents/data/grp/hst/cdbs"
os.environ['PYSYN_CDBS']=
# STEP 3
# SET YOUR OWN PATH to '/ABSCOEFF_CK/'
# e.g. mine is "/Users/meialua/Documents/data/ABSCOEFF_CK"
chimera_xsec_dir =
#STEP 4 picaso_refdata came in your clone so should be in this folder already
os.environ['picaso_refdata'] = os.path.join(os.getcwd(),'picaso_reference/')
# SET YOUR OWN PATH to 'opacities.db'
# e.g. mine is "/Users/meialua/Documents/data/opacities.db"
picaso_opacity_db =
import warnings
warnings.filterwarnings("ignore")
#python tools
import requests
import numpy as np
import pandas as pd
from bokeh.plotting import figure, show
import bokeh.palettes as color
from bokeh.io import output_notebook
from bokeh.layouts import row, column
output_notebook()
#double check that you have loaded BokehJS 2.1.1
What accuracy in planet properties do I need?¶
Using Exoplanet Archive API to Query Confirmed Targets¶
We can query from Exoplanet Archive to get a list of targets. Once we have all the targets we will have to narrow down the sample to only those that have suitable planet properties.
# use this default URL to start out with
default_query = "https://exoplanetarchive.ipac.caltech.edu/cgi-bin/nstedAPI/nph-nstedAPI?table=exoplanets&format=csv"
all_planets = requests.get(default_query)
all_planets = all_planets.text.replace(' ','').split('\n')
# default data doesn't come with all the parameters we need so let's
# add those in
add_few_elements = '&select='+all_planets[0]+','.join(
[',pl_trandur','pl_eqt','st_logg','st_metfe','st_j','st_h','st_k&'])
# use requests to grab the csv formatted data and split by the commas
all_planets = requests.get(default_query.split('&')[0]
+ add_few_elements + default_query.split('&')[1] )
all_planets = all_planets.text.replace(' ','').split('\n')
# get into useful pandas dataframe format
planets_df = pd.DataFrame(columns=all_planets[0].split(','),
data = [i.split(',') for i in all_planets[1:-1]])
planets_df = planets_df.replace(to_replace='', value=np.nan)
# convert to float when possible
for i in planets_df.columns:
planets_df[i] = planets_df[i].astype(float,errors='ignore')
#voila
planets_df.head()
Trouble finding what you are looking for?¶
#easy way to search through dataframe with many keys
[i for i in planets_df.keys() if 'mass' in i]
Get rid of everything without a mass¶
#let's only grab targets with masses and errors
pl_mass_err = planets_df.loc[:,['pl_bmassjerr1', 'pl_bmassj']].astype(float)
pl_mass_err = pl_mass_err.dropna()
Percentage of planets in NexSci database with masses
100*pl_mass_err.shape[0]/planets_df.shape[0]
Now let's get an idea of what those mass errors are
pl_mass_fig = figure(x_axis_type='log', width=550, height=400, x_axis_label='Mj',
y_axis_label='Mass Uncertainty',y_range=[0,150],x_range=[1e-3, 10])
pl_mass_fig.circle(pl_mass_err['pl_bmassj'],
100*pl_mass_err['pl_bmassjerr1']/pl_mass_err['pl_bmassj'],
color='black', size=5, alpha=0.5)
pl_mass_fig.outline_line_color='black'
pl_mass_fig.outline_line_width=3
pl_mass_fig.xgrid.grid_line_alpha=0
show(pl_mass_fig)
We only want targets with mass precision better than ~20%.
Let's also take only those targets that are brighter than J<12
#mass err less better than 20%
potential_props = pl_mass_err.loc[100*pl_mass_err['pl_bmassjerr1']/pl_mass_err['pl_bmassj']<20]
potential_props = planets_df.loc[pl_mass_err.index,:]
#brighter than 12
choose_from = potential_props.loc[potential_props['st_j']<12]
choose_from.shape[0]
What tools do I need? How do I use them?¶
Use PandExo to run initial constant $(R_p/R_*)^2$ to determine approx precision¶
Let's choose a single planet GJ 436 b as our example to evaluate observability.
Should'e already downloaded data: We won't go through the details of installation and default data. The conda environment on here should have installed PandExo. In order for this to work you will need to download the necessary default data. You can also go to the PandExo Installation Page.
#check to make sure it's in our list of nicely constained masses
choose_from.head()
# load pandexo
import pandexo.engine.justdoit as jdi
import pandexo.engine.justplotit as jpi
import pandexo.engine.bintools as bi
planet_name = 'GJ436b'
GJ436b = jdi.load_exo_dict(planet_name=planet_name)
For this initial run, the only 2 parameters you need to edit are:
Saturation level within the
observationkey: This will determine how many groups can fit with in an integration. Let's keep this at 80% to be safe.Change planet type to constant so that we don't have to input an atmospheric model yet.
GJ436b['planet']['type'] = 'constant'
GJ436b['planet']['f_unit'] = 'rp^2/r*^2'
GJ436b['observation']['sat_level'] = 80
GJ436b['observation']['sat_unit'] = '%'
Next pick an initial set of isntrument modes. I usually pick one at least one from each of the 4 (NIRISS, NIRSpec, NIRCam, and MIRI).
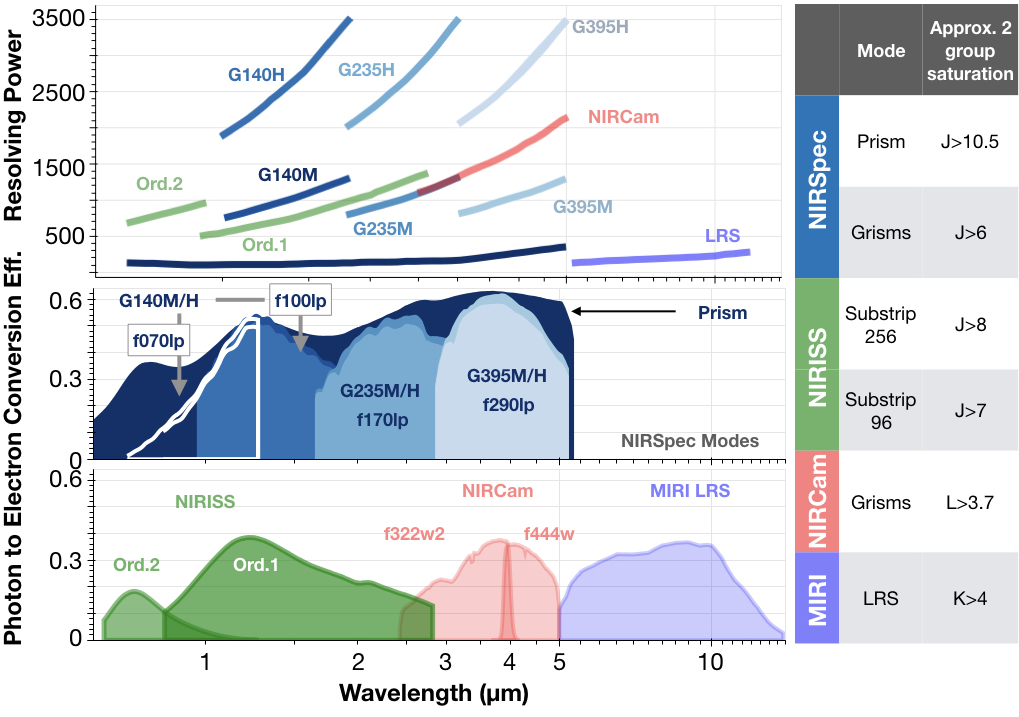
to_run = ['NIRISS SOSS', 'NIRSpec G395M', 'NIRCam F444W','MIRI LRS']
result = jdi.run_pandexo(GJ436b, to_run)
What is the approximate precision achieved by each observing mode in a single transit at native resolution??¶
prec_fig = figure(x_axis_type='log',y_range=[0,400],
height=300, x_axis_label='Wavelength(Micron)',
y_axis_label='Spectra Precision per pix (ppm)')
for i, inst in enumerate(to_run):
x = result[i][inst]['FinalSpectrum']['wave']
e = result[i][inst]['FinalSpectrum']['error_w_floor']*1e6 #PPM UNITS!
prec_fig.line(x,e, line_width=4, color = color.Colorblind6[i],legend_label=inst)
prec_fig.legend.location='top_left'
prec_fig.outline_line_color='black'
prec_fig.outline_line_width=3
prec_fig.xgrid.grid_line_alpha=0
prec_fig.ygrid.grid_line_alpha=0
show(prec_fig)
What is the approximate precision achieved by each observing mode in a single transit at $R = 100$ ??¶
from bokeh.io import reset_output
prec_fig = figure(x_axis_type='log',y_range=[0,200],
height=300, x_axis_label='Wavelength(Micron)',
y_axis_label='Spectral Precision ber R=100 bin (ppm)')
ES = {} # let's use this to store the values
XS = {}
for i, inst in enumerate(to_run):
if 'MIRI' not in inst:#LRS is already at around 100, so let's keep it at native R
x,y,e = jpi.jwst_1d_spec(result[i][inst], plot=False, model=False, R=100)
# if you check out your plot below you'll see the noise budget blows up at the
# detector edges so I usually make a 5*median cut to get rid of the crap
x = x[0][np.where(e[0]<5*np.min(e[0]))]
e = e[0][np.where(e[0]<5*np.min(e[0]))]*1e6 #PPM UNITS!
#plot
prec_fig.line(x,e, line_width=4, color = color.Colorblind6[i],legend_label=inst)
else:
x = result[i][inst]['FinalSpectrum']['wave']
e = result[i][inst]['FinalSpectrum']['error_w_floor']
x = x[np.where(e<5*np.min(e))]
e = e[np.where(e<5*np.min(e))]*1e6 #PPM UNITS!
prec_fig.line(x,e, line_width=4, color = color.Colorblind6[i],legend_label=inst)
#lets save these for later
XS[inst] = x
ES[inst] = e
prec_fig.legend.location='top_left'
prec_fig.outline_line_color='black'
prec_fig.outline_line_width=3
prec_fig.xgrid.grid_line_alpha=0
prec_fig.ygrid.grid_line_alpha=0
reset_output()
output_notebook()
show(prec_fig)
Use CHIMERA to determine first guess atmospheric transmission signal¶
From the PandExo exercise we've learned we can achieve approximately 30-50 ppm precision in a single transit. This is a great place to start. Now, we want to get a sense of what this data precision gives us, scientifically speaking.
This requires a transit model! For this tutorial we will use CHIMERA developed by Mike Line.
You should've already done: Chimera should have installed with your conda environment. You should have already downloaded the cross section folder and defined chimera_xsec_dir in Code Block 1.
import blackbox_codes as bbs #packaged function with chimera and picaso for the purposes of this demo !
Black box codes == there are many model parameters I am sweeping under the rug for the purposes of a clean and concise demo. With that cautionary note, we can proceed.
#this is a directory path where we will store our loaded stellar SEDs
stellar_dir = os.path.join(os.getcwd(),'stars')
First step for chimera will be to 1) load the cross section file, and 2) load in a stellar SED model.
Unfortunately NexSci doesn't always have all the necessary planet properties. If you get an error below, that is likely why. For GJ 436b, this is the case. NexSci is missing two values : Stellar Fe/H and Stellar effective temperature. I have added those two as kwargs which I found from Exo.MAST.
xsecs= bbs.grab_stars_xsecs(choose_from.loc[choose_from['pl_name']==planet_name],
chimera_xsec_dir, #defined in code cell 1
stellar_dir,
st_metfe = 0.02, st_teff=3479)
The simplest, most optimistic case: Cloud free, Solar Metallicity, Solar C/O¶
logMH = 0 #solar metallicity
logCO = -0.26 #solar carbon to oxygen ratio
wno, cloud_free, chemarr, y_binned = bbs.chimera_transit(
choose_from.loc[choose_from['pl_name']==planet_name], #note we can add planet_kwargs to fill
xsecs,logMH,logCO, pl_eqt=667) #in missing values
spec = figure(x_axis_type='log', y_axis_label='Relative Transit Depth',
x_axis_label='Wavelength(micron)',
height=300)
#mean subtracting your spectrum will help you understand your spectrum in the context of
#your noise simulations above. Here I am choosing to normalize to 1 micron.
cf_norm = 1e6*(cloud_free - cloud_free[np.argmin(np.abs(1e4/wno-1))])
spec.line(1e4/wno, cf_norm , color='black',line_width=3)
for i, inst in enumerate(to_run):
fake_y =np.interp( XS[inst], 1e4/wno[::-1],cf_norm[::-1] )
spec.varea(x=XS[inst],
y1=fake_y + ES[inst],
y2=fake_y - ES[inst] , alpha=0.7, color=color.Colorblind6[i])
show(spec)
This looks GREAT but highly sus. A water amplitude of 200pm at 1.4 $\mu$m means we could've easily detected something with Hubble. Was that the case? For this particular planet, we can check Exo.MAST to see if there is a transmission spectrum available.
Check Exo.MAST for available data so we can validate our assumptions¶
First, let's check to see if a transmission spectrum exists. We can use Exo.MAST!
Navigate to Exo.Mast, search for your planet and you should see a tab on the figure for "transmission spectra". The file below was taken from there.
IRL = pd.read_csv('GJ436b_transmission_Knutson2014.txt', skiprows=8,
names = ['micron','dmicron','tdep','etdep'], delim_whitespace=True)
Let's compare our real life data to what our optimistic 1xSolar cloud free case is.
#as we go through this, let's save our models in a dictionary
all_models = {}
spec = figure(x_axis_type='log', y_axis_label='Relative Transit Depth',
x_axis_label='Wavelength(micron)',
height=300)
#normalizing your spectrum will help you understand your spectrum in the context of
#your noise simulations above
cf_norm = 1e6*(cloud_free - cloud_free[np.argmin(np.abs(1e4/wno-1))])
all_models['1x'] = cf_norm
all_models['um'] = 1e4/wno
spec.line(1e4/wno, cf_norm , color='black',line_width=3)
#again mean subtract from value at 1 micron so they line up, and convert to ppm
y =1e6*( IRL['tdep'] - IRL.iloc[(IRL['micron']-1).abs().argsort()[0],2])
#plot the data
bbs.errorbar(spec, IRL['micron'], IRL['tdep']
, yerr = 1e6*IRL['etdep'] ,
#formatting
color='black',
point_kwargs={'size':5}, error_kwargs={'line_width':3})
for i, inst in enumerate(to_run):
fake_y =np.interp( XS[inst], 1e4/wno[::-1],cf_norm[::-1] )
spec.varea(x=XS[inst],
y1=fake_y+ ES[inst],
y2=fake_y - ES[inst] , alpha=0.7, color=color.Colorblind6[i])
show(spec)
The model is way off.
Proposals with 1xSolar cloud free claims are not realistic. What can we do to bolster our argument?¶
The data precision required to rule a 1xSolar CF model is not high enough. Therefore, if one bases their total observing time on a 1xSolar model, they would be largely under-asking for time. And, a TAC member might call out your proposal for having over simplified your model results.
Let's see what we can do to rectify this.
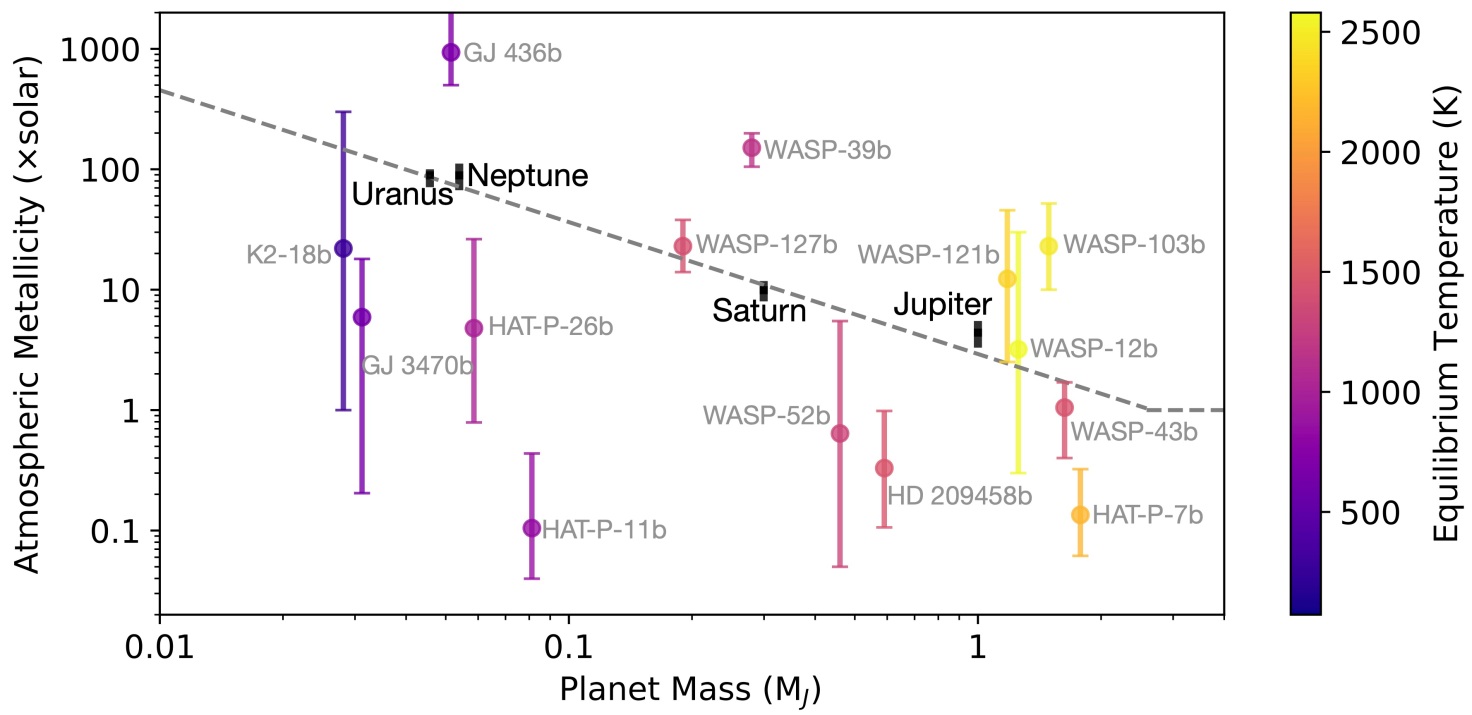
Try following the Mass-M/H plot to get a more "realistic" prediction of what the of M/H should be¶
In this case we have an estimate for GJ 436b already. But, let's pretend we don't have that yet :)
logMH = np.log10(200) #Solar metallicity taken by eye balling the Solar System fit #science
logCO = -0.26 #solar carbon to oxygen ratio
wno, cloud_free, chemarr, y_binned = bbs.chimera_transit(
choose_from.loc[choose_from['pl_name']==planet_name],
xsecs,logMH,logCO, pl_eqt=667)
Repeat the last exercise
#as we go through this, let's save our models
spec = figure(x_axis_type='log', y_axis_label='Relative Transit Depth',
x_axis_label='Wavelength(micron)',
height=300)
#normalizing your spectrum will help you understand your spectrum in the context of
#your noise simulations above
cf_norm = 1e6*(cloud_free - cloud_free[np.argmin(np.abs(1e4/wno-1))])
all_models['200x'] = cf_norm
spec.line(1e4/wno, cf_norm , color='black',line_width=3, legend_label='200xSolar')
spec.line(1e4/wno, all_models['1x'] , color='grey',line_width=3, legend_label='1xSolar')
#again mean subtract from value at 1 micron so they line up, and convert to ppm
y =1e6*( IRL['tdep'] - IRL.iloc[(IRL['micron']-1).abs().argsort()[0],2])
#plot the data
bbs.errorbar(spec, IRL['micron'], IRL['tdep']
, yerr = 1e6*IRL['etdep'] ,
#formatting
color='black',
point_kwargs={'size':5}, error_kwargs={'line_width':3})
for i, inst in enumerate(to_run):
fake_y =np.interp( XS[inst], 1e4/wno[::-1],cf_norm[::-1] )
spec.varea(x=XS[inst],
y1=fake_y+ ES[inst],
y2=fake_y - ES[inst] , alpha=0.7, color=color.Colorblind6[i])
spec.legend.location='top_left'
show(spec)
Looks much better already. Unfortunately we aren't done quite yet. The Mass-M/H trend is by no means ground truth.
Let's revisit our first hierarchical question:
- Can you detect an atmosphere?
The answer seems obvious: Of course!!! Two important questions must be addressed:
- At what level of significance?
- What about clouds?
- And other physical parameters? Temperature? C to O ratio?
We will visit these questions in Section 3: How can I prove observability.
But first, let's run some first guess emission cases.
Use PICASO to determine first guess atmospheric emission signal¶
We will switch gears to another package, PICASO, to play around with emission+reflected light.
Should've already downloaded PICASO data: Download the Resampled Opacity File from Zenodo. Create a variable defining where it is.
# load picaso
import picaso.justdoit as pj
import picaso.justplotit as pp
#load opacities
opas = pj.opannection(wave_range=[1,12], filename_db = picaso_opacity_db) #defined in code 1
#load planet in the same way as before
gj436_emis = pj.load_planet(choose_from.loc[choose_from['pl_name']==planet_name],
opas,
pl_eqt=667,st_metfe = 0.02, st_teff=3479)
# right now picaso and chimera are using a PT profile parameterization
# I've made sure they are the same for the purposes of this demo
T = gj436_emis.inputs['atmosphere']['profile']['temperature'].values
P = gj436_emis.inputs['atmosphere']['profile']['pressure'].values
The simplest case: Cloud free, Solar Metallicity, Solar C/O¶
For this demo we are going to use the same chemistry as chimera. Our little black body function contains the necessary function to grab the chemistry
all_emis = {}
# let's get the same chemistry as chimera for consistency
logMH = 0
logCO = -0.26
df_chimera = bbs.chimera_chem(logCO, logMH, T, P, xsects=xsecs)
#add in chemistry to picaso bundle
gj436_emis.atmosphere(df = df_chimera)
#run picaso
df_picaso = gj436_emis.spectrum(opas, calculation='thermal', full_output=True)
wno, fpfs = pj.mean_regrid(df_picaso['wavenumber'], df_picaso['fpfs_thermal'] , R=150)
Plot with our error bars from PandExo
spec = figure(x_axis_type='log', y_axis_label='Eclipse Spectrum (Fplanet/Fstar)',
x_axis_label='Wavelength(micron)',
height=300)
all_emis['1xSolar'] = fpfs*1e6
spec.line(1e4/wno, fpfs*1e6 , color='black',line_width=3)
for i, inst in enumerate(to_run):
fake_y =np.interp( XS[inst], 1e4/wno[::-1],fpfs[::-1]*1e6 )
spec.varea(x=XS[inst],
y1=fake_y + ES[inst],
y2=fake_y - ES[inst] , alpha=0.7, color=color.Colorblind6[i])
show(spec)
Wahoo! Since we don't have similar transmission data for emission spectroscopy, let's use our initial 200xSolar guess that we had for transmission to see the difference.
logMH = np.log10(200)
logCO = -0.26
df_chimera = bbs.chimera_chem(logCO, logMH, T, P, xsects=xsecs)
#add in chemistry to picaso bundle
gj436_emis.atmosphere(df = df_chimera)
#run picaso
df_picaso = gj436_emis.spectrum(opas, calculation='thermal', full_output=True)
wno, fpfs = pj.mean_regrid(df_picaso['wavenumber'], df_picaso['fpfs_thermal'] , R=150)
spec = figure(x_axis_type='log', y_axis_label='Eclipse Spectrum (Fplanet/Fstar)',
x_axis_label='Wavelength(micron)',
height=300)
spec.line(1e4/wno, all_emis['1xSolar'], color='grey',line_width=3, legend_label='1xSolar')
all_emis['200xSolar'] = fpfs*1e6
spec.line(1e4/wno, fpfs*1e6 , color='black',line_width=3, legend_label='200xSolar')
for i, inst in enumerate(to_run):
fake_y =np.interp( XS[inst], 1e4/wno[::-1],fpfs[::-1]*1e6 )
spec.varea(x=XS[inst],
y1=fake_y + ES[inst],
y2=fake_y - ES[inst] , alpha=0.7, color=color.Colorblind6[i])
spec.legend.location='top_left'
show(spec)
My first guess transmission and/or emission signals look promising. What's next?¶
Based on our initial 1x and 200x Solar models of transmission and emission, our simulations look great. So what is next?
We have to take our analysis one step further to determine at what level of significance we can make these detections.
How can I "prove" observability?¶
The classic hierarchical science levels are:
- Can you detect an atmosphere?
- Can you detect a specific molecule?
- Can you detect another physical process?
- Can you constrain a molecular abundance? A metallicity? A climate profile? An aerosol species?
This section will walk you through steps to determine where you stand on in this hierarchy.
Can an atmosphere be detected: Addressing cloud concerns and quantifying statistical significance in transmission¶
First, let's expand our initial 1xSolar M/H case. Let's add a few cloud cases (e.g. no cloud, medium cloud, high cloud) and a few M/H cases (e.g. 1x, 100x 1000x) and show first show how these relate to the expected data precision. Next we will discuss how to make these address our ability to detect (or not) each case.
MHs = [1, 10,100,700]
CLDs = [-27,-28,-29] #these are log cross sections which
all_models_trans = {i:{} for i in MHs}
fig = figure(height= 300,
x_axis_label='Wavelength(micron)',
y_axis_label='Relative Transit Depth (PPM)', x_axis_type='log')
colors = color.viridis(len(MHs)*len(CLDs))
ic = 0
for MH in MHs:
for CLD in CLDs:
logMH = np.log10(MH) #Solar metallicity taken by eye balling the Solar System fit #science
logCO = -0.26 #solar carbon to oxygen ratio
wno, model, chemarr, y_binned = bbs.chimera_transit(
choose_from.loc[choose_from['pl_name']==planet_name],
xsecs,logMH,logCO,logKcld=CLD, pl_eqt=667)
all_models_trans[MH][CLD] = 1e6*((model)- model[np.argmin(np.abs(1e4/wno-1))])
fig.line(1e4/wno, all_models_trans[MH][CLD] , color=colors[ic], line_width=3,
alpha=0.7,legend_label=str(MH)+str(CLD))
ic +=1
show(fig)
"Can an atmosphere be detected in transmission" usually translates to "can a $y=mx+b$ model be rejected"¶
fig = [figure(title = i, height= 250, width=300, x_axis_label='log Metallicity',
y_axis_label='log Cloud Cross Section', x_axis_type='log',
y_range=[-29.5,-26.5],x_range=[0.3,2e3]) for i in to_run]
#for our line model
from scipy.optimize import curve_fit
from scipy.stats.distributions import chi2
def line(x, a, b):
return a * x + b
all_ps = {i:[] for i in to_run}
for i, inst in enumerate(to_run):
for MH in MHs:
for CLD in CLDs:
y = all_models_trans[MH][CLD]
#wno is at lower res than our observation so we have to finagle them onto the same axis
binned_obs = bi.binning(XS[inst], XS[inst]*0, dy =ES[inst] ,newx=1e4/wno[::-1])
binned_model = bbs.instrument_tran_non_uniform(binned_obs['bin_x'],wno, y)[0]
binned_model = binned_model[~np.isnan(binned_model)]
#add random noise to your binned model which is now our "fake data"
fake_data = binned_model + np.random.randn(len(binned_obs['bin_dy']))*binned_obs['bin_dy']
#step 1) fit a line through each model
popt, pcov = curve_fit(line, binned_obs['bin_x'], fake_data, sigma =binned_obs['bin_dy'])
#now we have:
y_measured = fake_data
y_error = binned_obs['bin_dy']
y_line_model = line(binned_obs['bin_x'], popt[0], popt[1])
# .. and we can use tradition chi square p values to do some hypothesis testing
#compute chi square of each model
line_chi = np.sum((y_measured-y_line_model)**2/y_error**2)
p = chi2.sf(line_chi, len(y_measured) - 2)#2 because there are 2 free model params
all_ps[inst] += [[MH, CLD, p]]
#some crafy finagling to get a good color scheme
if p>0.05:
col = color.RdBu3[-1] #red if it cant be rejected
legend = 'Cannot Reject'
elif ((p<=0.05) & (p>=0.006)):
col = color.RdBu3[1] #white for medium/low rection
legend= 'Weak/Med Reject'
else:
col = color.RdBu3[0] #blue is strong rejection of line
legend='Strong Favor'
#hacked "heat map"
fig[i].square(MH, CLD, color = col, size=30,line_color='black',legend_label=legend)
show(column(row(fig[0:2]), row(fig[2:4])))
From these figures we can immediately come to a few conclusions
- NIRISS is most strongly impacted by clouds and has the least potential in being able to "detect an atmosphere" (e.g. reject a flat line hypothesis)
- NIRSpec and NIRCam are best at rejecting the flat line
- MIRI LRS struggles at rejecting flat line hypothesis
You can always create scenarios where an atmosphere is not detectable. For your proposal, it's only important to justify the level at which an atmosphere could be robustly detected.
Just for fun, with our saved dictionary from above:
bbs.write_justification(planet_name,all_ps)
Can an atmosphere be detected: Addressing unknown climate and quantifying statistical significance in emission¶
First, let's expand our initial 1xSolar M/H case. In transmission we focused on M/H and cloud cross sectional strength. Although clouds will have an ultimate effect on the emission spectra, the first order affect is that of the pressure-temperature profile. So here, instead of running through M/H-cloud parameter space, we are going to run through a few M/H-temperature cases.
Theorists Caution: To simplify this exercise we are parameterizing our pressure-temperature profiles. We urge groups to talk to their local theorist about the validity of this hack for your specific problem.
MHs = [1, 10,100,700]
DTs = [-100,0,100] #these are delta Kelvin amounts that we will use to perturb our PT profile
all_models_emis = {i:{} for i in MHs}
fig = figure(height= 300,
x_axis_label='Wavelength(micron)',
y_axis_label='Fp/Fs (PPM)', x_axis_type='log')
colors = color.viridis(len(MHs)*len(DTs))
ic = 0
for MH in MHs:
for DT in DTs:
logMH = np.log10(MH) #Solar metallicity taken by eye balling the Solar System fit #science
logCO = -0.26 #solar carbon to oxygen ratio
df_chimera = bbs.chimera_chem(logCO, logMH, T+DT, P, xsects=xsecs)
#add in chemistry to picaso bundle
gj436_emis.atmosphere(df = df_chimera)
#run picaso
df_picaso = gj436_emis.spectrum(opas, calculation='thermal', full_output=True)
wno_pic, fpfs = pj.mean_regrid(df_picaso['wavenumber'], df_picaso['fpfs_thermal'] , R=150)
#let's also save raw thermal flux (you'll see why next)
wno_pic, thermal = pj.mean_regrid(df_picaso['wavenumber'], df_picaso['thermal'] , R=150)
all_models_emis[MH][DT] = [fpfs*1e6,thermal]
fig.line(1e4/wno_pic, all_models_emis[MH][DT][0] , color=colors[ic], line_width=3,
alpha=0.7,legend_label=str(MH)+str(DT))
ic +=1
fig.legend.location='top_left'
show(fig)
"Can an atmosphere be detected in emission" usually translates to "can a blackbody model be rejected"¶
fig = [figure(title = i, height= 250, width=300, x_axis_label='log Metallicity',
y_axis_label='Delta T Perturbation', x_axis_type='log',
y_range=[-130,130],x_range=[0.3,2e3]) for i in to_run]
all_ps = {i:[] for i in to_run}
for i, inst in enumerate(to_run):
for MH in MHs:
for DT in DTs:
y_fpfs = all_models_emis[MH][DT][0]
y_fp = all_models_emis[MH][DT][1]
#wno is at lower res than our observation so we have to finagle them onto the same axis
binned_obs = bi.binning(XS[inst], XS[inst]*0, dy =ES[inst] ,newx=1e4/wno_pic[::-1])
#first get the binned Fp/Fs
binned_y_fpfs = bbs.instrument_tran_non_uniform(binned_obs['bin_x'],wno_pic, y_fpfs)[0]
binned_y_fpfs = binned_y_fpfs[~np.isnan(binned_y_fpfs)]
#how just the Fp (since we will be replacing this with a blackbody)
binned_y_fp = bbs.instrument_tran_non_uniform(binned_obs['bin_x'],wno_pic, y_fp)[0]
binned_y_fp = binned_y_fp[~np.isnan(binned_y_fp)]
#add random noise to your binned model which is now our "fake data"
fake_data = binned_y_fpfs + np.random.randn(len(binned_obs['bin_dy']))*binned_obs['bin_dy']
#just the star!
fstar_component = binned_y_fpfs / binned_y_fp
#blackbody function to fit for
def blackbody(x, t):
#x is wave in micron , so convert to cm
x = 1e-4*x
h = 6.62607004e-27 # erg s
c = 2.99792458e+10 # cm/s
k = 1.38064852e-16 #erg / K
flux_planet = np.pi * ((2.0*h*c**2.0)/(x**5.0))*(1.0/(np.exp((h*c)/(t*x*k)) - 1.0))
fpfs = flux_planet *fstar_component
return fpfs
#step 1) fit a line through each model
popt, pcov = curve_fit(blackbody, binned_obs['bin_x'], fake_data,p0=[100], sigma =binned_obs['bin_dy'])
#now we have:
y_measured = fake_data
y_error = binned_obs['bin_dy']
y_bb_model = blackbody(binned_obs['bin_x'], popt[0])
# .. and we can use tradition chi square p values to do some hypothesis testing
#compute chi square of each model
line_chi = np.sum((y_measured-y_bb_model)**2/y_error**2)
p = chi2.sf(line_chi, len(y_measured) - 1)#1 because we have t as the model param
all_ps[inst] += [[MH, DT, p]]
#some crafy finagling to get a good color scheme
if p>0.05:
col = color.RdBu3[-1] #red if it cant be rejected
legend = 'Cannot Reject'
elif ((p<=0.05) & (p>=0.006)):
col = color.RdBu3[1] #white for medium/low rection
legend= 'Weak/Med Reject'
else:
col = color.RdBu3[0] #blue is strong rejection of line
legend='Strong Favor'
#hacked heatmap
fig[i].square(MH, DT, color = col, size=30,line_color='black',legend_label=legend)
show(column(row(fig[0:2]), row(fig[2:4])))
From these figures we can immediately come to a few conclusions
- NIRISS doesn't cover adequate wavelengths to capture our planet's emission spectrum
- NIRSpec and NIRCam are best at rejecting the blackbody
- MIRI LRS is unable to differentiate high metallicity cases from a blackbody. This is a surprising result as you might suspect MIRI would always be best at thermal emission. Remember that MIRI precision was a bit higher in our first PandExo exercises.
Revisiting the 4 questions¶
Now that we've gone through our first observability test, we can revisit our 4 questions.
- Can you detect an atmosphere? Yes! And we've provided rigorous tests to determine the relevant parameter space.
- Can you detect a specific molecule?
- Can you detect another physical process?
- Can you constrain a molecular abundance? A metallicity? A climate profile? An aerosol species?
Can a specific molecule be detected?¶
There are a few ways to tackle this question. We are going to determine if it is possible to solely detect CH4 in a 100xSolar model. The easiest way to do is to simply remove the opacity contribution from the molecule in question.
Theorists Caution: You can always expand this to determine molecule detectability with different M/H, clouds, temperatures, etc.
Detecting CH4 Molecules in Transmission versus Emission¶
logMH = np.log10(100) #Solar metallicity taken by eye balling the Solar System fit #science
logCO = -0.26 #solar carbon to oxygen ratio
wno, trans_no_ch4, chemarr, y_binned = bbs.chimera_transit(
choose_from.loc[choose_from['pl_name']==planet_name],
xsecs,logMH,logCO,exclude_mol=['CH4'],
pl_eqt=667)
trans_no_ch4 = 1e6*((trans_no_ch4)- trans_no_ch4[np.argmin(np.abs(1e4/wno-1))])
figt = figure(height= 250, width=600,
x_axis_label='Wavelength(micron)',
y_axis_label='Relative Transit Depth (PPM)', x_axis_type='log')
figt.line(1e4/wno, trans_no_ch4, line_width=3, color='pink',
legend_label='Remove CH4')
figt.line(1e4/wno, all_models_trans[100][-29], line_width=3, color='black',
legend_label='Full Model')
Now (similar to our line analysis) we determine if the chi-square of our no-CH4 model
logMH = np.log10(100) #Solar metallicity taken by eye balling the Solar System fit #science
logCO = -0.26 #solar carbon to oxygen ratio
df_chimera = bbs.chimera_chem(logCO, logMH, T, P, xsects=xsecs)
#add in chemistry to picaso bundle
gj436_emis.atmosphere(df = df_chimera, exclude_mol=['CH4'])
#run picaso
df_picaso = gj436_emis.spectrum(opas, calculation='thermal', full_output=True)
wno_pic, fpfs_no_CH4 = pj.mean_regrid(df_picaso['wavenumber'],1e6*df_picaso['fpfs_thermal'] , R=150)
fige = figure(height= 250,width=600,
x_axis_label='Wavelength(micron)',
y_axis_label='Relative Transit Depth (PPM)', x_axis_type='log')
fige.line(1e4/wno_pic, fpfs_no_CH4, line_width=3, color='pink',
legend_label='Remove CH4')
fige.line(1e4/wno_pic, all_models_emis[100][0][0], line_width=3, color='black',
legend_label='Full Model')
show(column(figt, fige))
To attach statistical significance to how well CH4 can be detected in 100xSolar model, one can now repeat the line/blackbody analysis to compute and compare the $\chi^2$ of the "removed CH4" model against the "fake data" -- in this case, the fake data would include the contribution from CH4. If the "removed CH4" model cannot be strongly rejected then that molecule cannot be detected.
Revisiting the 4 questions¶
- Can you detect an atmosphere? Yes! And we've provided rigorous tests to determine the relevant parameter space.
- Can you detect a specific molecule? Yes!
- Can you detect another physical process?
- Can you constrain a molecular abundance? A metallicity? A climate profile? An aerosol species?
Question (3) can be approached in an identical manner to that of question (2). One interesting analysis would be to determine if a temperature inversion is detectable in emission.
Can any physical parameters be constrained? Information content theory for initial constraint estimates¶
The content below was created from the methodology described in Batalha & Line (2017) and Batalha et al. 2018. This methodology should not be used to replace retrievals as it cannot capture non-Gaussian posteriors (e.g. degenerate solutions, upper limits). However, it does offer a first order look at how well parameters can be constrained.
IC Theory Terminology¶
model, F(x): In this case the models we are looking at are spectral models. In particular,
CHIMERAandPICASOproduce:$F(x)$ = $(\frac{R_p}{R_s})_\lambda^2$ or $(\frac{F_p}{F_s})_\lambda^2$
state vector: this is the x in F(x). Usually there are dozens of values that go into this vector: e.g. planet radius, stellar radius, cloud properties, opacities, chemical abundances. In Batalha & Line 2017 we made the simple assumption that:
$x = [T_{iso}, log C/O, log M/H, \times R_p]$
Of course, this is an over simplification, but usually these are the properties we are interested in retrieving. I would encourage the user to start simple like this and expand from there.
Step 1) Computing Jacobians via finite differencing¶
Jacobians (K) describe how sensitive the mode is to slight perturbations in each state vector $x_a$ parameter at each wavelength place. Given our model above the Jacobian can be computed via:
$K_{ij} = \frac{\partial F_i(\mathbf{x})}{\partial x_j} = \begin{bmatrix} \partial F_{\lambda,1}/ \partial T & \partial F_{\lambda,1}/ \partial logC/O & \partial F_{\lambda,1}/ \partial logM/H & \dots & \dots \\ \partial F_{\lambda,2}/ \partial T & \partial F_{\lambda,2}/ \partial logC/O & \dots & \dots & \dots \\ \dots & \dots & \dots & \dots & \dots \\ \partial F_{\lambda,i}/ \partial T & \dots & \dots & \dots & \partial F_{\lambda,m}/ \partial x_j \end{bmatrix}$
Since we can't compute these partial derivatives analytically, we must do it numerically. Let's use a simple center finite differencing method. Going back to calculus, we have to calculate our partial derivatives about one state vector. Which, makes sense intuitively. You should expect your model to behave differently for hot temperature, high C/O planets than for low temperature, low C/O planets.
For example, let's say our center point is:
$x_0 = [T_{0}, log C/O_0, log M/H_0, xR_p]$ = [500, -.26, 0,1]
$\frac{\partial F_{\lambda,1}}{ \partial T }$ = $\frac{F([T_{iso,+1}, log C/O_0, log M/H_0, \times R_{p0}]) - F([T_{iso,-1}, log C/O_0, log M/H_0, \times R_{p0}])}{T_{+1} - T_{-1}}$
Where $T_{+1}$ and $T_{-1}$ are usually computed around $T_{-1} = T_{0} - (0.001*T_{-1})$
Because these jacobians are so specific to the $x_0$ about which they are computed. It's important to do your analysis for a wide range in temperatures, C/Os, M/Hs or whatever else you are interested in
#decide on a state vector. going to simplify greatly and only look at a
#two parameter state vector of M/H =200xsolar and C/O=solar
sv = {'logMet':2,'logCtoO':-0.26}
#now we have to specify how much we want perturb each parameter (this is the 0.001 number above)
#let's start with 1e-3. Later we can check if our value is sensitive to this
perturb = {'logMet':1e-3,'logCtoO':1e-3}
First, M/H Jacobian¶
# jacobian MH
MHp1 = np.log10(perturb['logMet']*(10.0**sv['logMet'])*np.log(10.0)+ (10.0**sv['logMet']))
MHm1 = np.log10(10.0**sv['logMet']- perturb['logMet']*(10.0**sv['logMet'])*np.log(10.0))
mh_jacobian = {i:[] for i in to_run} #save for each instrument
ys = []
for imh in [MHp1, MHm1]:
wno, model, chemarr, y_binned = bbs.chimera_transit(
choose_from.loc[choose_from['pl_name']==planet_name],
xsecs,imh,sv['logCtoO'],
pl_eqt=667)
ys += [1e6*(model - model[np.argmin(np.abs(1e4/wno-1))])]
#subtract the two and divide by delta (remember we are perturbing
# dF / dlogMH)
dFdMH = (ys[0] - ys[1])/(2.0*perturb['logMet'])
#now bin to different isntrument modes of interest
for inst in to_run:
binned_obs = bi.binning(XS[inst], XS[inst]*0, dy =ES[inst] ,newx=1e4/wno[::-1])
binned_model = bbs.instrument_tran_non_uniform(binned_obs['bin_x'], wno, dFdMH)[0]
binned_model = binned_model[~np.isnan(binned_model)]
mh_jacobian[inst] = binned_model
Next, C/O Jacobian¶
# jacobian MH
COp1 = np.log10(perturb['logCtoO']*(10.0**sv['logCtoO'])*np.log(10.0)+ (10.0**sv['logCtoO']))
COm1 = np.log10(10.0**sv['logCtoO']- perturb['logCtoO']*(10.0**sv['logCtoO'])*np.log(10.0))
co_jacobian = {i:[] for i in to_run} #save for each instrument
ys = []
for ico in [COp1, COm1]:
wno, model, chemarr, y_binned = bbs.chimera_transit(
choose_from.loc[choose_from['pl_name']==planet_name],
xsecs,sv['logMet'],ico,
pl_eqt=667)
ys += [1e6*(model - model[np.argmin(np.abs(1e4/wno-1))])]
#subtract the two and divide by delta (remember we are perturbing
# dF / dlogMH)
dFdCO = (ys[0] - ys[1])/(2.0*perturb['logCtoO'])
#now bin to different isntrument modes of interest
for inst in to_run:
binned_obs = bi.binning(XS[inst], XS[inst]*0, dy =ES[inst] ,newx=1e4/wno[::-1])
binned_model = bbs.instrument_tran_non_uniform(binned_obs['bin_x'], wno, dFdCO)[0]
binned_model = binned_model[~np.isnan(binned_model)]
co_jacobian[inst] = binned_model
Step 2) Build Prior Matrix¶
Information content is measured in bits and describes how the state of knowledge has increased.. RELATIVE to the prior. Therefore we must describe what our knowledge is before we make our observation. In most cases, there is none!! So we want to make these very large.
In this case pre-proposal, you likely have little information. Let's make our priors on M/H and C/O $\pm$ 6. Since we are in log units, these are very large numbers, which equate to having no prior information.
#diagonal matrix with priors on diag
prior = np.matrix(np.diag(np.array([6,6])**2))
Step 3) Build Error Covariance Matrix¶
The error covariance matrix describes our precision at each wavelength channel. This is where PandExo comes into play. We are going to assume that our noise has no correlations between wavelengths. Therefore, all we have to do is turn our PandExo runs into diagonal matrices. If there were correlations, the off-diagonal elements would be non-zero.
covariance = {i:[] for i in to_run}
for inst in to_run:
binned_obs = bi.binning(XS[inst], XS[inst]*0, dy =ES[inst] ,newx=1e4/wno[::-1])
covariance[inst] = np.matrix(np.diag(binned_obs['bin_dy']**2)) #remember to square as this is covariance
Step 4) Compute IC and other useful stats¶
- Posterior Covaraince, $\mathbf{\hat{S}}$, describes uncertanties and correlations of the atmospheric state vector after the measurement is made
$\mathbf{\hat{S}} = (\mathbf{K^TS_e^{-1}K + S_a^{-1}})^{-1}$
- Gain, $G$, describes the sensitivity of the retrieval to the observation (e.g. if $G=0$ the measurements contribute no new information
$\mathbf{G} = \mathbf{\hat{S}}\mathbf{K^TS_e^{-1}}$
- Averaging Kernel, $A$, tells us which of the parameters have the greatest impact on the retrieval
$\mathbf{A} = \mathbf{GK}$
Degrees of Freedom, is the sum of the diagonal elements of A tells us how many independent parameters can be determined from the observations
Total information content, $H$, is measured in bits and describes how our state of knowledge has increased due to a measurement, relative to the prior. This quantity is best used to compare and contrast modes.
$H = \frac{1}{2} \ln (|\mathbf{\hat{S}}^{-1}\mathbf{S_a}|)$
for inst in to_run:
jac = np.zeros((len(mh_jacobian[inst]), len(sv)))
jac[:,0] = mh_jacobian[inst]
jac[:,1] = co_jacobian[inst]
jac = np.matrix(jac)
s_hat = (jac.T*covariance[inst].I*jac + prior.I).I
gain = s_hat * jac.T * covariance[inst].I
A = gain*jac
DOF = float(A.trace())
H = 0.5*np.log(np.linalg.det(s_hat.I*prior))
print(inst)
print([list(sv.keys())[i]+'='+str(sv[list(sv.keys())[i]])+'+/-'+str(np.sqrt(s_hat[i,i]))[0:4]
for i in range(len(sv))])